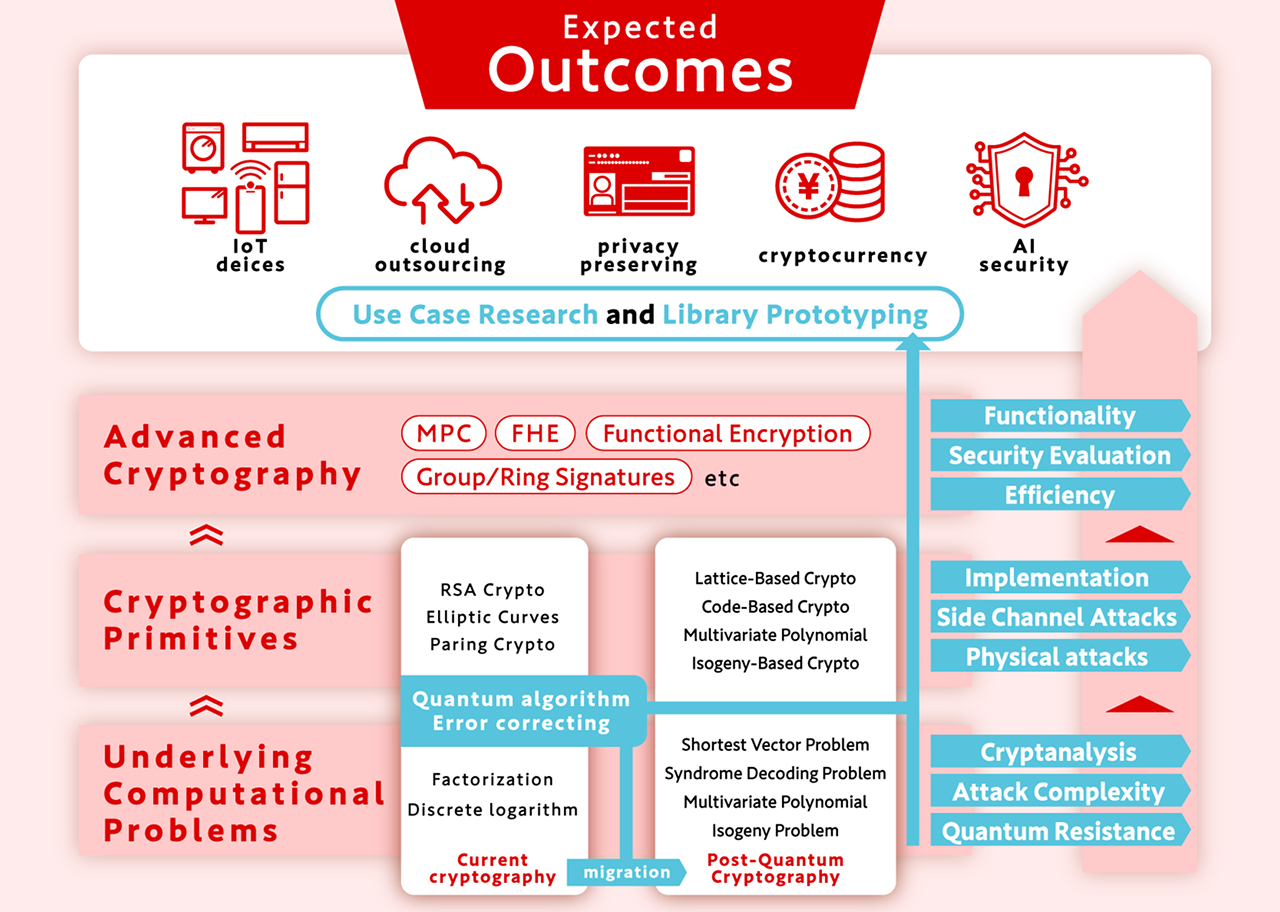
Cryptographic technology became widely adopted on the internet in the 1990s, as RSA encryption and elliptic curve cryptography were implemented in cryptographic communication software such as SSL/TLS. Since then, advances in information technology have enabled the use of cryptography in a wide range of contexts, including IoT devices, cloud environments, privacy protection, cryptocurrencies, and AI security. Furthermore, in the 2000s, the mathematical properties of bilinear pairings enabled the realization of advanced cryptographic schemes—known as advanced cryptography—that provide capabilities such as identity-based encryption, which were previously considered difficult to construct efficiently. In the realm of advanced cryptography, proposals have been made for fully homomorphic encryption and functional encryption for encryption schemes; blind signatures and ring signatures for digital signatures; and secret computation and distributed encryption using threshold secret sharing. These technologies now make it possible to perform computation on encrypted data and to achieve digital signatures that preserve the anonymity of the signer.
On the other hand, RSA cryptosystem, elliptic curve cryptography, and pairing-based cryptography are known to become vulnerable due to the fact that the underlying hard problems—the integer factorization problem and the discrete logarithm problem—can be solved efficiently by large-scale quantum computers. In response to this threat, the National Institute of Standards and Technology (NIST) in the United States launched a
standardization project for post-quantum cryptography in 2016. The major approaches under consideration include lattice-based cryptography, code-based cryptography, multivariate polynomial cryptography, and isogeny-based cryptography. These post-quantum cryptographic schemes are constructed based on the computational hardness of problems such as the shortest vector problem, the syndrome decoding problem, the multivariate polynomial problem, and the isogeny problem. The mathematical properties of these problems significantly influence not only the security and efficiency of the cryptographic schemes, but also their ability to support advanced functionalities.